前言

卷积神经网络（Convolutional Neural Network,CNN或ConvNet）是一种具有局部连接、权重共享等特性的深层前馈神经网络。卷积神经网络最早可以追溯到1970年代，但目前所说的CNN是源自Yann LeCun等人的工作。 CNN是近年来在计算机视觉领域取得突破性成果的基石，在自然语言处理、推荐系统和语音识别领域广泛使用。首先描述卷积神经网络中的卷积层和池化层的工作原理，并解释填充、步幅、输入通道和输出通道的含义。在掌握这些基础知识后，将展示一个简单的CNN网络实例（Python代码），接着探究几个具有代表性的深度卷积神经网络的设计思路，最后将对最新的关于CNN的论文进行研究和编码学习。

1 历史与问题

卷积神经网络是一种专门用来处理具有类似网络结构的数据的神经网络。例如时间序列数据（可以认为是在时间轴上有规律地采样形成的一维网格）和图像数据（可以看成二维的像素网格）。卷积网络在诸多应用领域都表现优异。“CNN”一词表明该网络使用了卷积（convolution）这种数学运算。卷积是一种特殊的线性运算。卷积网络是指那些至少在网络的一层使用卷积运算来替代一般的矩阵乘法运算的神经网络。 卷积神经网络最早是主要用于处理图像信息。若使用全链接前馈网络来处理图像，会存在以下两个问题：

（1）参数太多：如果输入图像大小为$100\times 100 \times3$（即图像的高度是100，宽度为100，3个颜色通道：RGB）。在全连接前馈神经网络中，第一个隐藏层的每一个神经元都有$100\times 100 \times3 = 30000$个相互独立的连接，每个连接都对应这一个权重参数。随着隐藏层神经元的增加，参数的规模也会急剧增加。这导致整个神经网络的训练效率会很低，也易出现过拟合。

（2）局部不变性特征：自然图像处理中的物体具有局部不变性特征，在尺寸缩放、平移、旋转等操作上不影响其语义信息。全连接网络很难提取这些局部不变性特征，一般需要进行数据增强来提高性能。

2 整体框架

CNN由几个基本的层构成，这些层包括输入层、卷积层、池化层、全连接层和输出层所构成，如下图1所示，其模块化的表示如图2所示。输入层、全连接层和输出层工作原理先不叙述，待以后整体叙述时补上。卷积层和池化层是CNN的核心。 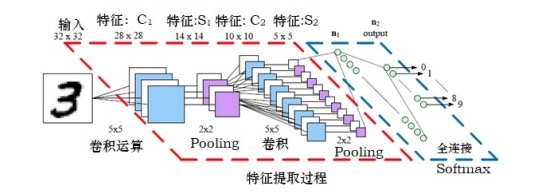图1 CNN的架构

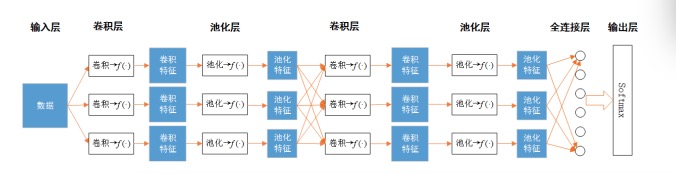图2 CNN的基本模块

3 卷积层

卷积层是CNN中最重要部分，包含多个特征映射，卷积层中的每个特征映射相当于之前所述网络的节点，特征映射通过卷积运算和激活函数$f(\cdot)$将输入映射为卷积特征。每个特征映射可接收一个或多个前层特征输入，并包含与特征输入数目相同的卷积滤波器（也称为卷积核）。这些卷积滤波器与输入时行卷积运算，然后将结果通过激活函数后，输出卷积特征。

3.1 卷积与卷积滤波器

当以$2-D$特征$a$作为输入时，卷积滤波器$w$是二维的矩阵。令输入特征$a$和卷积滤波器$w$分别为 $$ a = \begin{pmatrix} 1 & 3 & 0 & -1 \ -2 & 0 & 3 & 2 \ 2 & -3 & -1 & 4 \ 4 & 2 & 0 & 1 \end{pmatrix} w = \begin{pmatrix} 3 & -1 \ 0 & 2 \end{pmatrix} $$
进行卷积运算时，先对滤波器$w$进行$180^{\circ}$翻转，得到
$$ \tilde{w} = \begin{pmatrix} 2 & 0 \-1 & 3 \end{pmatrix} $$
然后按照图3所示进行计算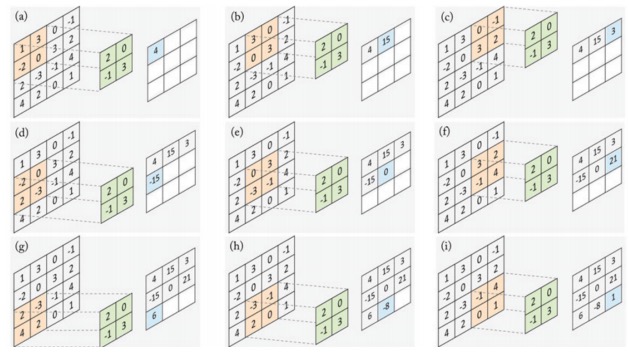
图3 卷积计算过程

卷积运算就是$a*w$的过程，计算过程展示如下
$$ \begin{pmatrix} 1 & 3 & 0 & -1 \ -2 & 0 & 3 & 2 \ 2 & -3 & -1 & 4 \ 4 & 2 & 0 & 1 \end{pmatrix} * \begin{pmatrix} 3 & -1 \ 0 & 2 \end{pmatrix} = \begin{pmatrix} 4 & 15 & 3 \-15 & 0 & 21 \6 & -3 & 1 \end{pmatrix} $$

3.2 机器学习中的卷积运算

1）卷积定义

卷积运算定义为:
$$ z=aw \qquad z(i,j)=(aw)(i,j)=\sum_{m}\sum_{n}a(m,n)w(i-m,j-n) $$
由于卷积是可交换的，因此上式可等价地写作
$$ z=wa \qquad z(i,j)=(aw)(i,j)=\sum_{m}\sum_{n}a(i-m,j-n)w(m,n) $$

2)卷积与互相关

互相关的计算方式与卷积几乎相同但没有对滤波器进行翻转
$$ z(i,j)=(a*w)(i,j)=\sum_{m}\sum_{n}a(i+m,j+n)w(m,n) $$
在机器学习中采用卷积和互相关所得到的结果一致，因此不对两者进行区分。

3）卷积与矩阵乘法

离散卷积可看成矩阵乘法，即$z=Wa=w*a$，其中$W$是由滤波器$w$得到的$Toeplitz$矩阵，对于二维情况，$W$是由滤波器$a$得到的双重分块循环矩阵。此外还有
$$ W^{T}b=\tilde{w}*b $$
其中$\tilde{w}$表示对滤波器$w$进行翻转，即旋转$180^{\circ}$，其所对应的Matlab代码为$Rot90(w,2)$。
例：从$w$得到$Toeplitz$矩阵
$$ w=(-1,1) \implies W=\begin{pmatrix} -1 &1& 0 &\cdots&0 \ 0&-1&1&\cdots&0 \ \vdots&\vdots&\vdots&\ddots&\vdots \ 0&0&0&\cdots&1 \end{pmatrix} $$

3.3滤波器的输出和三种卷积

滤波器在输入特征的水平与垂直方向上的移动位置称为滤波器的步长（stride），默认为$s=1$。为了获得不同大小的卷积输出，可对输入特征$a$在水平与垂直方向上进行补零（zero-padding），即在输入特征$a$的两个方向上分别补上$p$个$0$.比如对
$$ a = \begin{pmatrix} 1 & 3 & 0 & -1 \ -2 & 0 & 3 & 2 \ 2 & -3 & -1 & 4 \ 4 & 2 & 0 & 1 \end{pmatrix} $$
进行$p=2$的补0，得到
$$ a = \begin{pmatrix} 0&0&0&0&0&0&0&0\ 0&0&0&0&0&0&0&0\ 0&0&1 & 3 & 0 & -1&0&0 \ 0&0&-2 & 0 & 3 & 2&0&0 \ 0&0&2 & -3 & -1 & 4&0&0\ 0&0&4 & 2 & 0 & 1&0&0\ 0&0&0&0&0&0&0&0\ 0&0&0&0&0&0&0&0\ \end{pmatrix} $$
假定输入特征的大小为$m\times n$，卷积滤波器的大小为$f\times f$,卷积运算的步长为$s$，$zero-padding$的大小为$p$,则输入特征与滤波器的卷积输出为
$$ h^{'}=\lfloor \frac{h-f+s+p}{s} \rfloor \ w^{'}=\lfloor \frac{w-f+s+p}{s} \rfloor $$
依据使用不同的补0方式，有是三种卷积：
a) 'valid'卷积：不对输入特征$a$进行补0处理，卷积运算都在输入特征$a$的有效范围内进行。这种卷积输出$z$的大在水平和垂直方向分别减少了$f-1$，其中$f$是卷积滤波器$w$的大小。

b) 'same'卷积：输出和输入的大小相同。需对输入$a$进行 $p=\lfloor f/2\rfloor$

c) 'full'卷积：对输入特征$a$采用最大可能的补0，即$p=f-1$，其中$f$为卷积滤波器$w$的大小。

注：CNN在信息正向传播时使用‘valid’型卷积，在反向传播算法中使用‘full’型的卷积。

3.4 局部感受野和共享参数

感受野（Receptive Field） 主要是指听觉、视觉等神经系统中一些神经元的特性，即神经元只接受其所支 配的刺激区域内的信号。在视觉神经系统中，视觉皮层中的神经细胞的输出依 赖于视网膜上的光感受器。视网膜上的光感受器受刺激兴奋时，将神经冲动信 号传到视觉皮层，但不是所有视觉皮层中的神经元都会接受这些信号。一个神 经元的感受野是指视网膜上的特定区域，只有这个区域内的刺激才能够激活该 神经元。
局部感受野：将局部感受野的窗口沿着整个图像从左到右、从上到下滑动，可以得到一系列局部感受野。每个局部感受野对应隐藏层的一个不同的隐藏节点，如下图所示。对$28\times 28$的输入图像采用$5\times 5$的局部感受野，得到一个含有$24\times 24$的隐藏层。

图4 局部感受野与隐藏层节点
指的是所有隐藏层的节点采用相同的权值和偏置。例如：在隐藏层共有$24\times 24$个节点，每个节点对应的网络参数为$5\times 5$个加权参数和一个偏置参数$b$。也就是说网络的参数不是$24\times 24\times (5\times 5 + 1)$个参数，而是$5\times 5 + 1$个参数。隐藏层的第$j,k$个节点的输出为
$$ a_{j,k}=f(\sum^{4}{l=0}\sum^{4}{m=0}w_{l,m}x_{j+l,k+m}) $$
参数共享意味着隐藏层所有的节点有输入图像的不同位置来检测的是相同的特征。因此，CNN具有平移不变性。
通常也将由输入层到隐藏层的映射称为特征映射，共享的加权参数和偏置也被称为核或滤波器。
例：一组滤波器（局部感受野的加权参数）能够检测图像（$28\times 28$）中的一种特征类型的特征（$24\times 24$），并实现一种由原始输入到隐藏层特征的映射。输入的图像包含多种不同的局部特征，因此对应需要多组不同的滤波器，以实现多种不同的特征映射，如图5所示。在这个例子中包含了3个滤波器，从而实现了三种不同的特征映射。每个滤波器输出对应一个隐藏层（$24\times 24$）。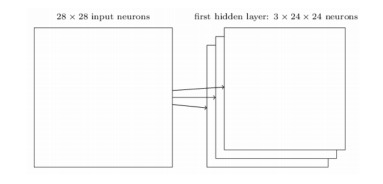

图7 含有多个滤波器的输出（卷积层）的CNN
共享参数的一个好处是其极大地减少了网络参数。每个特征映射仅需要$25=5\times 5$个加权和一个偏置参数，即26个参数。若有20个特征映射，则参数总数为$30\times 26=780$个参数。若采用全连接网络，以$28\times 28$大小为输入，含有30个隐藏层节点，其参数为$780\times 30=23550$个参数。也就是说，全连接网络参数的数量是CNN的30倍。

鸣谢

[1] Aston Zhang,Mu Li,Zachary C.Lipton,Alexander J.Smola.动手学深度学习.2019-05-13

[2] Shi-wen Deng.深度学习讲义.2018-02-26

[3] 邱锡鹏.神经网络与深度学习.2019-04-04

[4] Ian Goodfellow,Yoshua Bengio,Aaron Courville.Deep Learning.2017-09-14[汉译版]

接 ▶️ 《卷积神经网络简述》（第二篇）

本文首次发布于 ZhaoYLng Blog, 作者 @Laqudee ,转载请保留原文链接.