上一篇 ▶️ 《卷积神经网络》（第一篇）

前言

时间隔了好久的亚子......
都忘记了......

4 池化（pooling）层

4.1 简述

通过卷积获得特征[features]后，下一步将利用获取的特征去做分类。但面临着计算了庞大的挑战。例如：一个$96 \times 96$像素的图像，假设我们已经学习得到了400个定义在$8 \times 8$输入上的特征，每一个特征和图像卷积都会得到一个$(96-8+1) \times (96-8+1) = 7921$维的特征，由于有400个特征，所以每个样本例[example]都会得到一个$89^2 \times 400 = 3168400$维的卷积特征向量。当特征N非常大时，非常难以计算，且易出现过拟[over-fitting]。注：每个卷积模版生成一个特征，每个特征是$89^2$维。

为了解决这个问题，采取了一种叫做“池化”的操作，平均池化或者最大池化。

若选择图像中连续范围作为池化区域，并且只是池化相同的隐藏单元产生的特征，那么这些池化单元就具有平移不变性[translationinvariant]。

• 形式化描述：
  • 在获取到卷积特征后，确定池化区域的大小，来池化卷积特征。将卷积特征划分到数个大小相等不相交的区域，取该区域的平均值或者最大值来表示该区域的特征。池化后的特征便可以用来做分类。

4.2 pooling层的实现方法

CNN中，卷积层后接pooling层。pooling层对卷积层输出信息进行简化。与卷积层类似，需要指定池化区域的大小和步长。

• 假定输入特征的大小维 $h \times w$
• 池化区域的大小维 $f \times f$
• 步长为$s$

则池化运算的输出大小为：

$$ h^{'} = \lfloor \frac{h-f+s}{s} \rfloor \ w^{'} = \lfloor \frac{w-f+s}{s} \rfloor $$

例如，当输入特征a为

$$ a = \begin{pmatrix} 1 & 3 & 0 & -1 \ -2 & 0 & 3 & 2 \ 2 & -3 & -1 & 4 \ 4 & 2 & 0 & 1 \end{pmatrix} $$

以$2 \times 2$为pooling区域大小、步长为1时的max-pooling运算过程。得到的池化输出为：

$$ \begin{pmatrix} 3&3&3 \ 2&3&4 \ 4&2&4 \end{pmatrix} $$

池化操作可有效地对输入的特征实现采样，从而获得紧凑的特征表示。去除那些不显著的特征位置，从而进一步减少了参数个数。

Max pooling 运算示意图


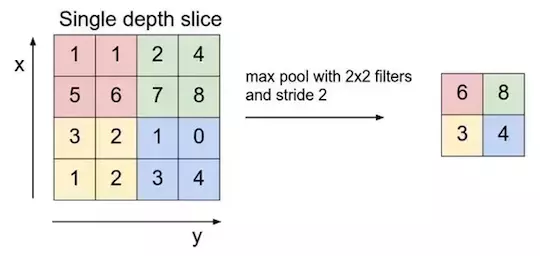由于卷积层包含多个特征映射[一个映射对应一个卷积滤波器]，max-pooling需要应用于每个特征映射。若包含是那个特征映射的池化过程，会得到三个max池化输出。

CNN手绘图


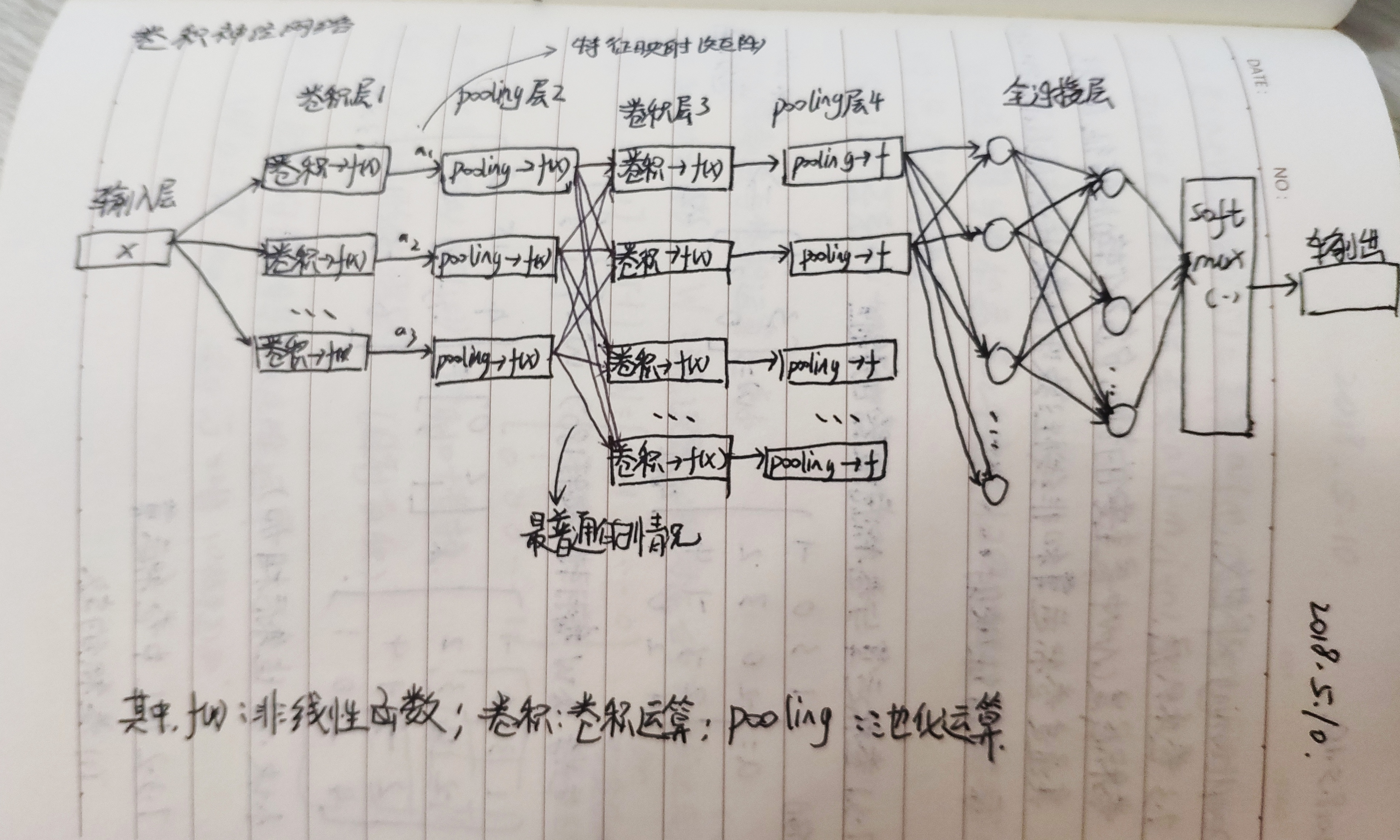5 全连接层

在CNN架构的末端是全连接层，即在全连接层中的每一个节点与上一层所有节点都连接。全连接层可以有多个，这类似于前馈神经网络中的隐藏层，然后连接到输出层，如含有Softmax、SVM的输出层，完成分类任务。

6 简化架构CNN的训练方法

CNN可以包含多个层，这些层主要包括下面三种：卷积层、Pooling、全连接层。

所谓简化，指的是卷积层的每个输出特征只使用一个卷积滤波器与前一层的一个输出生成。训练方法则分为信息的正向传播和反向传播过程。

6.1 卷积层[Convolution Layers]

（1）信息在卷积层的正向传播
假定CNN中的当前第$l$层为卷积层，其前一层的输出为$a_{l-1} \in R^{N \times N}$，所使用的卷积滤波器（此处假定只使用一个滤波器）为$w \in R^{N \times N}$，则卷积层的输出为$a_{l} \in R^{(N-m+1) \times (N-m+1)}$。在此层的信息传播过程简述为：

$$ a_{l-1} \underrightarrow{\quad w \quad} z_{l} \underrightarrow{\quad f(\cdot ) \quad} a_{l} $$

其包含如下两个过程：
1）第$l$层的净输入为

$$ z_{l} = w \ast a_{l-1} + b11^{T} $$

其中$\ast$表示二维卷积运算，其所对应的Matlab代码为：

z_l = conv2(w, a_l_1, 'valid') + b
//此处使用的卷积方式为‘valid’

2）非线性输出

$$ a_{l} = f(z_{l}) $$

（2）卷积层参数$w$和$b$学习
假定网络的代价函数为$J(\cdot)$，采用反向传播算法来更新网络参数需要计算两个参数的梯度，即$\nabla_{w}J$和$\nabla_{b}J$。令$\delta_{l}$表示由反向传播算法传递到当前第$l$层的残差，即$\delta_{l} = \nabla_{z_{l}}J = D[J;z_{l}]^{T}$。

1）$w$关于$J(\cdot)$的梯度：$\nabla_{w}J$
求微分

$$ \begin{aligned} d(J ; \omega) &=\operatorname{Tr}\left(D\left[J ; \mathrm{z}{\ell}\right] d\left(\mathrm{z}{\ell} ; \omega\right)\right) \ &=\operatorname{Tr}\left(\delta_{\ell}^{T} d\left(\mathrm{z}{\ell} ; \omega\right)\right) \ &=\operatorname{Tr}\left(\delta{\ell}^{T} d\left(\omega * \mathrm{a}{\ell-1}\right)\right) \ &=\operatorname{Tr}\left(\mathrm{a}{\ell-1} * \delta_{\ell}^{T} d \omega\right) \end{aligned} $$

从而得到

$$ \nabla_{w}J = \delta_{l} \ast \tilde{a}{l-1} = \tilde{\delta}{l} \ast a_{l-1} $$

其中$\tilde{B}$表示将$B$旋转$180^{\circ}$，即

$$ \left[\begin{array}{l}{1,2} \ {3,4}\end{array}\right] \rightarrow\left[\begin{array}{l}{4,3} \ {2,1}\end{array}\right] $$

所对应的Matlab代码为

nabla_w_J = conv2(a_l_1, rot90(delta_l, 2), 'valid');

2）$b$关于$J(\cdot)$的梯度：$\nabla_{b}J$
求微分

$$ \begin{aligned} d(J ; \omega) &=\operatorname{Tr}\left(D\left[J ; \mathbf{z}{\ell}\right] d\left(\mathbf{z}{\ell} ; b\right)\right) \ &=\operatorname{Tr}\left(\delta_{\ell}^{T} \mathbf{1} \mathbf{1}^{T}\right) d b \ &=\mathbf{1}^{T} \delta_{\ell} \mathbf{1} d b \end{aligned} $$

因此

$$ \nabla_{b} = 1^{T} \delta_{l}1 $$

6.2 Pooling层

（1）Pooling函数
Pooling层对输入应用Pooling函数作为输出。Pooling函数使用某一位置的相邻输出的总体统计特征来代替网络在该位置的输出。给定pooling层的一个pool中的节点$[x_{i}]_{i=1}^{N}$，常用的两种Pooling函数定义为：

max-pooling

$$ \psi(\mathbf{x})=\max {i} \mathbf{x}{i} $$

average pooling

$$ \psi(\mathbf{x})=\frac{1}{N} \sum_{i=1}^{N} \mathbf{x}_{i} $$

（2）信息的正向传播
假定当前层$l$是Pooling层，作为Pooling层可以没有参数，因此没有参数需要更新，它只是将输出数据的维度按照某种方式变小了。Pooling 层的输入为$a_{l-1}$，其输出$a_{l}$可表示为

$$ a_{l} = down(a_{l-1}) $$

其中$down(\cdot)$表示下采样函数。

当然也可以引入非线性激活函数$f(\cdot)$和Pooling层参数$\beta$(乘性偏置)及$b$(加性偏置)，则Pooling层得到如下输出

$$ \mathbf{a}{\ell}=f\left(\beta \operatorname{down}\left(\mathbf{a}{\ell-1}\right)+b \mathbf{1} \mathbf{1}^{T}\right) $$

（3）Pooling层参数学习
令$z_{l}=\beta down(a_{l-1})+b11^T$和$\delta_{l}=\nabla_{z_{l}}J$。

1）参数$\beta$的梯度
微分

$$ \begin{aligned} d(J ; \beta) &=\operatorname{Tr}\left(D\left[J ; \mathbf{z}{\ell}\right] d(\mathbf{z} ; \beta)\right) \ &=\operatorname{Tr}\left(\delta{\ell}^{T} \operatorname{down}\left(\mathbf{a}_{\ell-1}\right)\right) d \beta \end{aligned} $$

得到梯度

$$ \nabla_{\beta} J=\operatorname{Tr}\left(\delta_{\ell}^{T} \operatorname{down}\left(\mathbf{a}{\ell-1}\right)\right)=\mathbf{1}^{T}\left(\delta{\ell} \circ \operatorname{down}\left(\mathbf{a}_{\ell-1}\right)\right) \mathbf{1} $$

这里利用了$Tr(A^{T}B) = 1^{T}(A \circ B)1$.

2)参数$b$的梯度
求微分

$$ \begin{aligned} d(J ; b) &=\operatorname{Tr}\left(D\left[J ; \mathbf{z}{\ell}\right] d(\mathbf{z}, b)\right) \ &=\operatorname{Tr}\left(\delta{\ell}^{T} \mathbf{1} \mathbf{1}^{T}\right) d b \end{aligned} $$

得到梯度

$$ \nabla_{b}J = 1^{T}\nabla_{l}1 $$

6.3 残差$\delta_{l}$的反向传播

卷积层和Pooling层参数更新都需要使用反向传播的残差$\delta_{l}$。然而，$\delta_{l}$的传播与网络的上层有关。CNN通常架构为：

$$ \text{输出层} \rightarrow \text{卷积层} \rightarrow \text{Pooling层} \rightarrow \text{卷积层} \rightarrow \text{Pooling层} \rightarrow \cdot \cdot \cdot \rightarrow \text{全连接层} \rightarrow \text{输出层} $$

（1）卷积层残差$\delta_{l}$：经Pooling层传播得到
在卷积层参数更新所用的残差$\delta_{l}$是由Pooling层的残差$\delta_{l+1}$反向传播回来的，其信息的正向传播的网络结构关系为

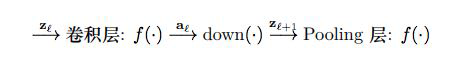
首先，需要先确定卷积层净输入$z_{l}$与Pooling层净输入$z_{l+1}$间的关系（复合函数关系），然后，利用复合函数的求导关系来确定卷积层残差$\delta_{l}$和Pooling层残差$\delta_{l+1}$间的关系。

信息的正向传播过程为

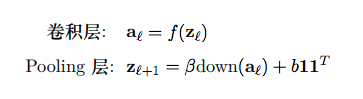
由于存在着下采样运算$down(\cdot)$，从而使得$a_{l}$中的一个大小为$n \times n$的块对应$z_{l+1}$中的一个元素。可通过定义上采样$up(\cdot)$将Pooling层的信息传播写作

因此

$$ \delta_{l} = \nabla_{z_{l}}J = \beta(up(\delta_{l+1})\circ f^{'}(z_{l})) $$

这是残差经过Pooling层的反向传递过程。

（2）Pooling层残差$\delta_{l}$：经卷积层得到
Pooling层参数更新所用到的残差$\delta_{l}$是由卷积层的残差$\delta_{l+1}$反向传播得到的，其信息的正向传播的网络结构关系为：

上式所对应的Matlab代码为

delta_l = conv2(rot90(w,2), delta_l_1_plus, 'full') circ df(z_l)
//这里所用的卷积方式是'full'

「我系🐦」

接 ▶️ 《卷积神经网络简述》（第三篇）

通俗易懂的CNN介绍

鸣谢

[1] Shi-wen Deng.深度学习讲义.2018-02-26

[2] Ian Goodfellow,Yoshua Bengio,Aaron Courville.Deep Learning.2017-09-14[汉译版]

本篇笔记首次发布于 Laqudee.Z Blog, 作者 @Laqudee ,转载请保留原文链接.